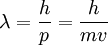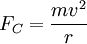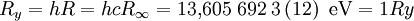Rydberg-Konstante

Die Rydberg-Konstante ${\displaystyle R_{\infty }}$ ist eine nach Johannes Rydberg benannte Naturkonstante. Sie tritt in der Rydberg-Formel auf, einer Näherungsformel zur Berechnung von Atomspektren. Ihr Wert ist die als Wellenzahl ausgedrückte Ionisierungsenergie des Wasserstoffatoms unter Vernachlässigung relativistischer Effekte und der Mitbewegung des Kerns (also bei unendlicher Kernmasse, daher der Index ${\displaystyle \infty }$).

Der derzeit empfohlene Wert der Rydberg-Konstante beträgt:

${\displaystyle R_{\infty }=10\,973\,731{,}568\,157(12)\,\mathrm {m} ^{-1}.}$

Die relative Standardunsicherheit beträgt 1,9 · 10⁻¹².

Zusammenhang mit anderen Naturkonstanten

Die Rydberg-Konstante ist mit der Feinstrukturkonstante α, dem bohrschen Radius a₀ und der Compton-Wellenlänge λ_C,e des Elektrons wie folgt verknüpft:

${\displaystyle R_{\infty }={\frac {\alpha ^{2}}{2}}\,{\frac {1}{\lambda _{\mathrm {C,e} }}}={\frac {\alpha ^{2}}{2}}\,{\frac {m_{\mathrm {e} }c}{h}}={\frac {m_{\mathrm {e} }e^{4}}{8c\varepsilon _{0}^{2}h^{3}}}={\frac {\alpha }{4\pi a_{0}}}}$

Hierbei ist

• ${\displaystyle m_{\mathrm {e} }}$ die Masse des Elektrons,
• ${\displaystyle c}$ die Lichtgeschwindigkeit,
• ${\displaystyle h}$ die Planck-Konstante,
• ${\displaystyle e}$ die Elementarladung,
• ${\displaystyle \varepsilon _{0}}$ die elektrischen Feldkonstante.

Rydberg-Frequenz und Rydberg-Energie

Die Rydberg-Konstante wird häufig auch als Frequenz oder als Energie angegeben. Die empfohlenen Werte betragen:

• Rydberg-Frequenz: ${\displaystyle R=c\,R_{\infty }=3{,}289\,841\,960\,2500(36)\cdot 10^{15}\,\mathrm {Hz} }$
• Rydberg-Energie: ${\displaystyle R_{y}=h\,R=h\,c\,R_{\infty }=2{,}179\,872\,361\,030(24)\cdot 10^{-18}\,\mathrm {J} =13{,}605\,693\,122\,990(15)\,\mathrm {eV} =1\,\mathrm {Ry} .}$

Der konkrete Wert der Rydberg-Energie ${\displaystyle R_{y}}$ wird als Maßeinheit für Energien verwendbar.

Herleitung

Eine erste Herleitung der Rydberg-Konstante ${\displaystyle R_{\infty }}$ konnte im Rahmen des Bohrschen Atommodells gegeben werden. Eine modernere Herleitung im Rahmen der Quantenmechanik findet sich im Wasserstoffproblem.

In beiden Fällen gelangt man zu einer Formel für die quantisierten Energieniveaus des Wasserstoffatoms von der Form:

${\displaystyle E_{n}=-{\frac {m_{\mathrm {e} }e^{4}}{8\varepsilon _{0}^{2}h^{2}}}\cdot {\frac {1}{n^{2}}}}$

Aus der Differenz zweier Energieniveaus

${\displaystyle \Delta E=-{\frac {m_{\mathrm {e} }e^{4}}{8\varepsilon _{0}^{2}h^{2}}}\left({\frac {1}{n_{2}^{2}}}-{\frac {1}{n_{1}^{2}}}\right)}$

lässt sich mit

${\displaystyle \Delta {E}={\frac {hc}{\lambda }}}$

die Wellenzahl des bei einem solchen Übergang emittierten oder absorbierten Lichtes bestimmen zu

${\displaystyle {\frac {1}{\lambda }}={\frac {m_{\mathrm {e} }e^{4}}{8\varepsilon _{0}^{2}h^{3}c}}\left({\frac {1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right).}$

Der Vergleich mit der Rydberg-Formel zeigt, unter der Annahme eines unendlich schweren Wasserstoffkerns, dass die Rydberg-Konstante gegeben ist durch

${\displaystyle R_{\infty }={\frac {m_{\mathrm {e} }e^{4}}{8\varepsilon _{0}^{2}h^{3}c}}.}$

Daraus ergibt sich auch, dass die Rydberg-Konstante die Wellenzahl (inverse Wellenlänge) eines Photons ist, dessen Energie der Ionisierungsenergie des Wasserstoffatoms entspricht.

Weblinks

Einzelnachweise